NILAI MUTLAK
Kelas: X MIPA 2
No.Absen: 31
NILAI MUTLAK
https://saintif.com/persamaan-nilai-mutlak/
Pengertian Nilai Mutlak
Semua bilangan mempunyai nilai mutlak nya masing masing. Semua bilangan mutlak bernilai positif, sehingga nilai bilangan mutlak dari bilangan dengan angka yang sama namun beda notasi positif (+) dan negatif (-) akan mempunyai hasil bilangan mutlak yang sama.
Jika x anggota dari bilangan riil, maka nilai mutlak ditulis dengan |x| dan didefinisikan sebagai berikut:
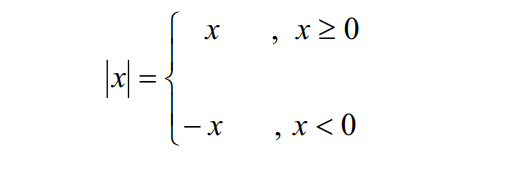
“Nilai mutlak merupakan bilangan dengan nilai yang sama dari panjang atau jarak dari titik asal atau titik nol dalam koordinat.”
Hal ini dapat diartikan dengan nilai mutlak dari 5 adalah panjang atau jarak dari titik 0 hingga ke titik 5 maupun (-5).
Nilai mutlakk dari (-9) dan 9 adalah 9. Nilaii mutlak 0 adalah 0, dan begitu seterusnya. Nilaa
i mutlak akan lebih mudah dipahami dengan melihat gambar berikut:
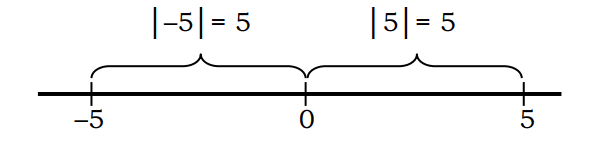
Pada gambar diatas, dapat dipahami bahwa nilai dari |5| adalah jarak titik 5 dari angka 0 yaitu 5, dan |-5| jarak titik (-5) dari angka 0 yaitu 5.
Jika |x| menyatakan jarak dari titik x ke 0, maka |x-a| merupakan jarak titik x ke titik a. Sebagai contoh, ketika dinyatakan jarak titik 5 ke titik 2 dapat ditulis dengan |5-2|=3
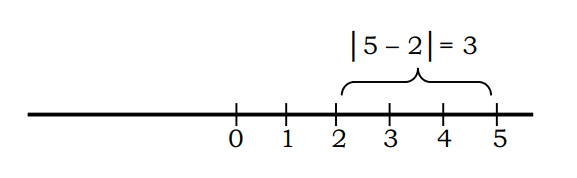
Secara umum dapat dinyatakan bahwa jarak x ke a dapat dituliskan dengan notasi |x-a| atau |a-x|

Sebagai contoh yaitu, jarak suatu bilangan ke titik 3 senilai 7 dapat digambarkan berikut:

Jika diuraikan dalam persamaan aljabar |x-3|=7 dapat diselesaikan sebagai berikut:
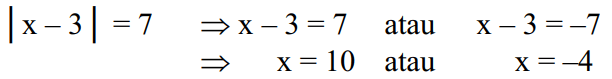
Ingat, bahwa |x-3| adalah jarak bilangan x ke titik 3, dengan |x-3|=7 adalah jarak bilangan x ke titik 3 sepanjang 7 satuan.
Sifat-sifat Nilai Mutlak
Pada operasi persamaan bilangan mutlak, terdapat sifat-sifat bilangan mutlak yang dapat membantu menyelesaikan persamaan bilangan mutlak.
Berikut sifat-sifat angka mutlak pada umumnya pada persamaan nilaii mutlak:
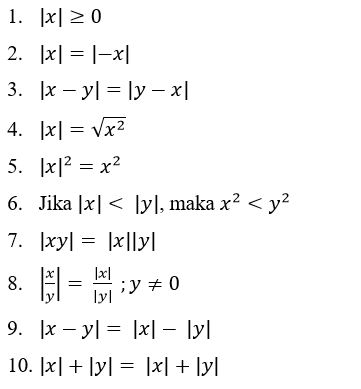
Sifat-sifat nilai mutlak pada pertidaksamaan:
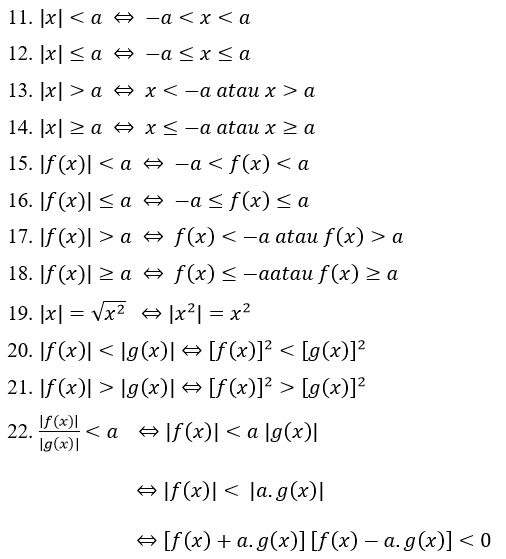
Contoh Soal Persamaan Nilai Mutlak
Contoh Soal 1
Berapa hasil x untuk persamaannilai mutlak |x-6|=10?
Jawab:
Untuk menyelesaikan persamaan tersebut, terdapat dua kemungkinan hasil bilangan mutlak
|x-6|=10
Solusi pertama:
x-6=10
x=16
solusi kedua:
x – 6= -10
x= -4
Jadi, jawaban untuk persamaan ini yaitu 16 atau (-4)
Contoh Soal 2
Selesaikan dan hitunglah nilai x pada persamaan berikut
–3|x – 7| + 2 = –13
Jawab:
–3|x – 7| + 2 = –13
–3|x – 7| = –13 – 2
–3|x – 7| = –15
|x – 7| = –15/ –3
|x – 7| = 5
Selesai sampai solusi diatas, maka nilai x mempunyai dua nilai
x – 7=5
x=12
atau
x – 7 = – 5
x=2
sehingga hasil akhir nilai x adalah 12 atau 2
Contoh Soal 3
Selesaikan persamaan berikut dan berapa nilai x
|7 – 2x| – 11 = 14
Jawab:
|7 – 2x| – 11 = 14
|7 – 2x| = 14 + 11
|7 – 2x| = 25
Selesai pada persamaan diatas, maka bilangan untuk nilai mutlak x adalah sebagai berikut
7 – 2x = 25
2x = – 18
x= – 9
atau
7 – 2x = – 25
2x = 32
x = 16
Sehingga hasil akhir nilai x adalah (– 9) atau 16
Contoh Soal 4
Tentukan penyelesaian dari persamaan nilaimutlak berikut:
|4x – 2| = |x + 7|
Jawab:
Untuk menyelesaikan persamaan diatas, menggunakan dua kemungkinan peyelesaian yaitu:
4x – 2 = x + 7
x = 3
atau
4x – 2 = – ( x + 7)
x= – 1
Jadi penyelesian persamaan |4x – 2| = |x + 7| adalah x = 3 atau x= – 1
Contoh Soal 5
Tentukan penyelesaian persamaan nilaimutlak berikut:
|3x+2|²+|3x+2| – 2=0
Berapa nilai x?
Jawab:
Penyederhanaan : |3x+2| = p
maka
|3x+2|²+|3x+2|-2=0
p² + p – 2 = 0
(p+2) (p – 1) = 0
p+2 = 0
p = – 2 (nilai mmutlak tidak negatif )
atau
p – 1 = 0
p = 1
|3x+2| = 1
Sampai pada penyelesaian diatas, maka terdapat 2 kemungkinan jawaban untuk x, yaitu:
3x+2 = 1
3x = 1 – 2
3x = – 1
x = – 1/3
atau
– (3x+2) = 1
3x+2 = – 1
3x = – 1 – 2
3x = – 3
x = – 1
Jadi penyelesaian persamaan tersebut adalah x= – 1/3 atau x= – 1
Komentar
Posting Komentar